La sua storia – ottimamente descritta da (Brigaglia, Masotto, 1982) – sempre oscillante tra caratterizzazione nazionale e forti aspirazioni internazionali, la personalità del nobile palermitano allievo di Cremona e il suo incredibile successo testimoniano la vivacità del sistema matematico italiano. Al “Circolo”, congiuntamente alla sezione matematica dell'Accademia dei Lincei, viene affidata l'organizzazione del quarto Congresso internazionale dei matematici tenutosi a Roma nel 1908. A questa data il Circolo ha un ruolo realmente internazionale: dei suoi 924 soci, i 2/3 (ben 618) sono stranieri! I servizi che esso offre sono di alta qualificazione professionale: una rivista internazionale e un suo supplemento che raccoglie gli indici di oltre 80 riviste specializzate e una vasta bibliografia. Il suo prestigio internazionale è unanimamente riconosciuto e Henri Poincaré (1854-1912) nel 1908 scrive, su Le Temps, che il Circolo è senz'altro la più importante organizzazione matematica mondiale.
Una lettera di HENRI POINCARÉ al quotidiano “LE TEMPS” sul IV Congresso Internazionale dei Matematici
Altrettanto positivo è il giudizio sulla formazione e il reclutamento, che avviene anche a livello della comunità allargata ai docenti delle scuole secondarie e che si giova del fatto che la prima generazione, quella dei Beltrami, Betti, Brioschi, Casorati e Cremona, oltre a stabilire in prima persona importanti risultati, forma una seconda generazione estremamente brillante. Come ha sottolineato ancora di recente (Bottazzini, 1998, p. 59), si tratta di un gruppo di matematici che alla ricerca scientifica originale associa l'impegno nella vita politica del nostro paese.
Per descrivere con qualche dettaglio questa seconda generazione, già sostanzialmente delineata nel panorama delle scuole italiane più importanti presentato nella Parte II, conviene fare riferimento alla classica tripartizione della disciplina in Geometria, Analisi e Fisica matematica.
2. La scuola italiana di Geometria algebrica
I meriti della generazione risorgimentale (Betti, Brioschi, ecc.) vanno visti soprattutto in prospettiva, nella creazione di quelle condizioni che rendono possibile lo sviluppo di una seconda generazione che trasforma l'Italia matematica in una “grande potenza”, terza dopo la Francia e la Germania. È quello che possiamo chiamare il periodo aureo. Vi vedremo all'opera alcuni dei protagonisti degli anni tra le due guerre mondiali ed è con questa “eccellenza” che il periodo successivo si dovrà confrontare.
La prima menzione va alla scuola di Geometria algebrica. Il premio Bordin dell'Académie des Sciences, assegnato sia nel 1907 che nel 1909 a matematici italiani4, rappresenta il riconoscimento che la Geometria algebrica è diventata, per antonomasia, l'italienische Geometrie.
Allievo di Cremona5 è Giuseppe Veronese6 (1854-1917) che, tra il 1880 e il 1881, è a Berlino e a Lipsia dove entra in contatto con Felix Klein. È naturalmente un incontro importante: l'approccio strutturale del matematico tedesco orienta Veronese nello studio pioneristico dei fondamenti della Geometria non-archimedea e della Geometria proiettiva degli iperspazi. Allievo di Battaglini è, invece, Enrico D'Ovidio (1843-1933) che, trasferitosi a Torino, avvia alla ricerca il giovane Corrado Segre (1863-1924). Sarà lui che porterà – direttamente o tramite i suoi allievi – a piena maturità la Geometria algebrica italiana. È dalla sua scuola, lo si è detto, che si sviluppa quello studio delle superfici algebriche che sarebbe diventato il maggior vanto della tradizione italiana.
Segre7 esordisce con una notevole tesi di laurea sulle quadriche negli iperspazi e alcuni studi relativi alla loro geometria, seguendo gli orientamenti di Veronese. Ben presto le tecniche proiettive vengono messe “al servizio” di altre ricerche, che gli permettono di sviluppare il programma di A. Brill e M. Noether a proposito della geometria su una curva algebrica ovvero dello studio delle proprietà delle curve algebriche che risultano invarianti rispetto alle trasformazioni birazionali. Ugualmente rilevante è l'efficacia propulsiva del suo magistero con i famosi corsi di “Geometria superiore”, tenuti dal 1888 al 1924. La radicale contrapposizione tra Geometria e Analisi, ravvisabile nel purismo di Cremona, viene per certi versi superata ma sempre in una cornice che evidenzia la supremazia dei metodi sintetici. È la loro eleganza e produttività che si pone come modello per tutto l'edificio matematico. Sono tutti allievi di Segre, Guido Castelnuovo (1865-1952), Federigo Enriques (1871-1946) e Francesco Severi (1879-1961) con i quali solitamente la scuola italiana di Geometria algebrica viene identificata8. Sulle loro figure e la loro attività conviene spendere qualche parola in più: esordiscono brillantemente negli anni a cavallo tra i due secoli, ma li ritroveremo poi – magari in altri ambiti di ricerca – anche negli anni Trenta. Severi, in particolare, sarà una delle figure-chiave della Matematica italiana tra le due guerre mondiali.
Subito dopo la laurea a Padova – allievo di Veronese – Castelnuovo ottiene nel 1886 un posto di perfezionamento a Roma, per seguire le lezioni di Cremona. L'anno successivo lo troviamo a Torino, dove avvia una lunga e amichevole collaborazione con Segre. La sua ricerca riguarda per ora lo studio delle curve algebriche. La svolta si ha qualche anno dopo, nel '91, con il passaggio alla cattedra di Geometria dell'Università di Roma. È qui che diventa prevalente il nuovo studio delle superfici algebriche. È a Roma che Castelnuovo incontra Enriques, con cui scriverà pagine fondamentali nella storia della teoria delle superfici algebriche.
Enriques si era laureato nel '91 a Pisa. Voleva perfezionarsi a Torino con Segre. Quella che invece riesce ad ottenere è una prima sistemazione a Roma. Qui passa rapidamente dall'entourage dell'ormai anziano Cremona a quello dell'emergente Castelnuovo, che lo avvia appunto verso lo studio delle superfici algebriche. Già nel '93 e nel '96 – quando è a Bologna da due anni – Enriques pubblica due fondamentali Memorie, in cui pone le premesse per una loro teoria organica e una loro classificazione. Enriques non abbandonerà mai completamente questi studi – a differenza di Castelnuovo che, di fatto, terminerà le pubblicazioni di Geometria algebrica nei primi anni del secolo – anche se ben presto inserirà su questo filone una notevole sensibilità verso le Matematiche elementari (sviluppata anche grazie alla conoscenza personale di Felix Klein) e verso la filosofia e la storia della Matematica.
Il suo incontro con Castelnuovo, la loro amicizia (ulteriormente rafforzata quando Castelnuovo sposerà la sorella di Enriques) e i loro progetti scientifici sono documentati da un eccezionale carteggio9, che ospita le quasi 700 lettere scritte da Enriques a Castelnuovo tra il 1892 e il 1906. Le due personalità appaiono complementari: ad un Enriques vulcanico, che procede con una straordinaria potenza intuitiva, già quasi sicuro dell'esito cui perverrà per approssimazioni successive, meno interessato alle dimostrazioni e al loro rigore, impaziente e spesso distratto lettore degli articoli dei colleghi, si affianca un Castelnuovo forse meno brillante ma ugualmente originale e che si incarica anche di precisare e incanalare lungo binari più corretti e produttivi le geniali intuizioni del cognato. Dalla loro collaborazione, in vent'anni, nasce un nuovo modo di inquadrare la teoria delle superfici algebriche che porta ad una classificazione particolarmente semplice, con l'eliminazione di tutti i casi particolari. In due Note10 del 1914 Enriques espone i risultati pressochè definitivi: le superfici vengono suddivise in classi di equivalenze birazionali, in funzione dei valori assunti dai plurigeneri e dal genere numerico. La pubblicazione nello stesso anno di un lungo articolo11, firmato assieme a Castelnuovo, sulla Encyklopädie der Mathematischen Wissenshaften, rappresenta il coronamento di tutta la ricerca e il riconoscimento ufficiale della sua significatività da parte della comunità matematica internazionale.
Di Severi avremo modo di parlare diffusamente anche nel seguito di questa nostra narrazione, sia per le sue ricerche in Geometria algebrica sia per illustrare una personalità ricca e sfaccettata, che non disdegna interessi e interventi di carattere culturale e filosofico, sia ancora per il ruolo politico che eserciterà nel periodo tra le due guerre mondiali, come indiscusso leader dei matematici. Più giovane anche di Enriques, Severi si laurea nel 1900 a Torino con Segre. Due anni dopo lo troviamo a Bologna, assistente di Enriques, che ne orienta gli interessi verso la teoria delle superfici algebriche. Severi vincerà la cattedra già nel 1905, docente prima all'Università di Parma e subito dopo in quella di Padova. Sono del 1903 i primi segnali della sua attenzione, in particolare, verso le superfici irregolari. Si comincia a intravedere – sempre all'interno della scuola – una personalità forte e originale, con una più marcata attenzione verso gli aspetti topologici e funzionali. Severi “recupera” i metodi trascendenti12 per determinare, in particolare, il legame tra superfici irregolari e superfici dotate di integrali di differenziali totali di prima e seconda specie. Con Enriques i rapporti sono per il momento ottimi e la collaborazione continua: nel 1907, ai due matematici – come abbiamo anticipato – viene assegnato il premio Bordin. Severi, in particolare, riceve anche la Medaglia Guccia al Congresso internazionale di Roma, nel 1908, da parte di una commissione formata da M. Noether, H. Poincaré e C. Segre. Avvia, poi, il tentativo di estendere quei risultati e metodi, che si erano rivelati così efficaci nel caso delle superfici, allo studio delle varietà. Negli stessi anni viene eletto socio dell'Accademia dei Lincei, che nel 1913 gl assegnerà il Premio Reale.
Un cenno a parte meritano gli studi di Geometria differenziale. In realtà, i due ambiti di ricerca non sono così separati (come, per chiarezza, vengono qui presentati) e i nomi che figurano sono in parte gli stessi. Due però sono nuovi: Luigi Bianchi (1856-1928) e Gregorio Ricci-Curbastro (1853-1925). Entrambi si laureano a Pisa e entrambi passano un primo periodo di perfezionamento a Göttingen, con Klein. Non è la prima volta che incontriamo il nome del matematico tedesco; di fatto, Klein svolge un ruolo analogo a quello che Riemann aveva svolto con la prima generazione, confermando l'attrattiva che la Matematica tedesca e i suoi modelli organizzativi esercitano su quella italiana.
Bianchi trascorre tutta la sua vita matematica a Pisa, dove sarà Direttore della Normale dal 1918 al 1928. Scrive13 anche su argomenti di Analisi, di Algebra, di Teoria dei numeri e un suo primo notevole merito riguarda l'attività di trattatista. Sulle sue Lezioni di Geometria differenziale si formeranno intere generazioni di matematici italiani. Ugualmente meritoria è la sua opera didattica in campo algebrico, con monografie che divulgano in Italia le tecniche aritmetiche elaborate dalla scuola tedesca e, in particolare, da L. Kronecker, R. Dedekind, H. Weber e D. Hilbert. Per quanto riguarda più specificamente la Geometria differenziale, già nella tesi di abilitazione del 1879 Bianchi introduce la cosiddetta “trasformazione complementare” per superfici immerse nello spazio ordinario. Il risultato viene utilizzato nella teoria delle equazioni alle derivate parziali e, in particolare, per l'equazione non lineare che oggi si chiama sine-Gordon. Altre Note riguardano la teoria generale degli spazi riemanniani. In un lavoro14 del 1902 si trovano illustrate le cosiddette identità di Bianchi, soddisfatte dalle derivate covarianti dei simboli di curvatura di Riemann a quattro indici. Ma, nonostante l'uso della derivata covariante, come osserva L. Pizzochero15, Bianchi rimane sostanzialmente estraneo ai metodi del Calcolo assoluto.
Ne è dunque “padrone” assoluto, in Italia, Ricci-Curbastro che, dopo il rientro da Göttingen, si trasferisce definitivamente a Padova. Qui, nel decennio che va dal 1885 al 1895, pone le basi del calcolo tensoriale. Già nel 1886 una sua Nota introduce quelle che successivamente chiamerà derivate covarianti di una funzione. L’espressione compare per la prima volta in un lavoro dell'anno seguente: Ricci-Curbastro studia i sistemi covarianti a molti indici, prescrivendo per loro la classica legge di trasformazione sotto cambiamenti di coordinate. Una Memoria del 1888, con la comparsa dei sistemi a molti indici controvarianti, segna sostanzialmente la nascita del Calcolo assoluto con la modifica degli ordinari procedimenti del calcolo differenziale proposta in modo che formule e risultati conservino la stessa forma, qualunque sia il sistema di variabili impiegato. Le espressioni di Calcolo differenziale assoluto e di sistemi assoluti compaiono nella Memoria Méthodes de calcul différential absolu et leur application, scritta con il suo allievo Tullio Levi Civita (1873-1941) e pubblicata nel 1901 nei Mathematische Annalen suinvito di F. Klein. L'efficacia dei nuovi metodi sarà compresa con un certo ritardo. Il riconoscimento internazionale per Ricci-Curbastro arriverà solo alla vigilia della guerra: nel 1913, Einstein adotterà il Calcolo assoluto come il linguaggio matematico di base per quella teoria della Relatività generale che stava muovendo i primi passi16.
3. La Fisica-matematica
Adesso dobbiamo dare il giusto rilievo alla comparsa – quale allievo di Ricci Curbastro – di Levi-Civita, uno dei più creativi matematici italiani della prima metà del XX secolo. Il suo nome ritornerà spesso in questo volume.
Tullio Levi-Civita17 (1873-1941) si laurea a Padova e a Padova svolge tutta la prima parte della carriera accademica, con l'eccezione di un breve periodo di perfezionamento a Bologna (dove conosce Enriques, con cui stringe una lunga amicizia) e di un altro breve periodo di insegnamento a Pavia. Nel 1918 viene chiamato all'Università di Roma, prima come professore di Analisi superiore e poi di Meccanica razionale. Levi-Civita è essenzialmente un fisico matematico, i cui interessi spazieranno dall'Elettromagnetismo alla Meccanica analitica, da quella celeste alla Relatività, dall'Idrodinamica alla teoria del calore. In tutta la sua opera sarà presente – come hanno osservato L. Dell'Aglio e G. Israel18 – uno stretto connubio tra innovazione e tradizione, con la acquisizione dei punti di vista più nuovi e originali ma anche la fedeltà ad una prospettiva nella quale l'indagine analitica si sviluppa sulla base delle risultanze scaturite da un preliminare ricorso a modelli geometrici.
Nei primi anni della sua carriera, Levi-Civita sviluppa le ricerche sulla stabilità secondo Liapounov, dimostra il teorema (del 1901) sui moti stazionari e intraprende quegli studi sulla teoria della scia in Idrodinamica che avrebbe poi proseguito a Roma. In Meccanica celeste si dedica al classico problema dei tre corpi. Nel 1896 dà il primo fondamentale contributo al Calcolo assoluto19. È anche la prima occasione in cui il Ricci's Calculus viene inserito in un ambito estrinseco alla Geometria differenziale metrica, per un problema di Meccanica analitica. Un'altra e non meno significativa illustrazione della fecondità del Ricci's Calculus viene fornita da una Memoria20 di poco successiva (1899), con la ricerca dei tipi di potenziali che si possono far dipendere da due sole coordinate di spazio. Nello stesso anno – come abbiamo già ricordato – nel corso di un suo soggiorno a Padova Klein chiede a Levi-Civita di scrivere un compendio organico del calcolo tensoriale per i Mathematische Annalen21. Levi-Civita accettò l’offerta e scrisse insieme a Ricci l’articolo “Méthodes de calcul différentiel absolu et leurs applications”, considerato il manifesto dell'algebra tensoriale. Il contributo di Levi-Civita sarà essenziale non tanto nella formulazione del metodo, quanto nelle sue applicazioni alla fisica matematica. Le relazioni tensoriali non cambiano al variare del sistema di coordinate e quindi il loro linguaggio risulta particolarmente utile per esprimere quelle proprietà che sono, per loro natura, indipendenti dal riferimento scelto.
I lavori finora citati si riferiscono a un Levi-Civita ancora giovanissimo. Negli stessi anni è invece già molto alta la stella di Vito Volterra22 (1860-1940), leader indiscusso della comunità matematica italiana nei primi decenni del nuovo secolo. A Pisa, dove aveva studiato in particolare con Betti, si era laureato nel 1882. Diventa quindi professore nelle Università di Pisa e poi, di Torino. Nel 1901 si trasferisce definitivamente a Roma, succedendo a Beltrami. Il passaggio nella capitale intensifica la presenza di Volterra sulla scena pubblica e il suo coinvolgimento in ruoli di crescente responsabilità nella politica scientifica e culturale del Paese. All'inizio del secolo, Volterra è eletto presidente della Società Italiana di Fisica ; nel 1905, il primo ministro Giolitti inserisce il suo nome nell'elenco dei nuovi senatori del Regno; nel 1907 fonda la Società Italiana per il Progresso delle Scienze (SIPS) – di cui diventerà anche il primo presidente – sul modello di analoghe società già esistenti in Francia, Inghilterra e altri Paesi industrializzati, e con l'obiettivo di creare un punto di incontro tra scienziati di diverse aree e in occasione di divulgazione dei loro risultati. Avremo modo di parlare ripetutamente di Volterra. La sua personalità attraversa 50 anni della vita scientifica italiana e permetterà di trattare argomenti di Fisica matematica e di Analisi, ma anche di Economia matematica e di Dinamica delle popolazioni.
La differenza di età con Levi-Civita non raggiunge i 15 anni, ma contribuisce a radicare Volterra in una prospettiva più classica e “ottocentesca“, dove ancora più forte si avverte il richiamo di una ricerca fortemente unitaria, che riesce a descrivere la complessità dei fenomeni fisici macroscopici utilizzando poche equazioni di base. Per quanto concerne la Fisica matematica, i contributi più importanti, negli anni a cavallo tra i due secoli, riguardano la propagazione della luce nei mezzi birifrangenti, gli spostamenti dei poli terrestri (o, per essere più precisi, i moti della superficie terrestre rispetto all'asse di rotazione della Terra), i fenomeni ereditari e quella che nel linguaggio moderno viene chiamata teoria delle dislocazioni. Quest'ultima – Volterra usa il termine di distorsioni – si colloca in quella teoria dell'elasticità che, nel giudizio di Klein, era diventata la “questione nazionale” degli italiani. Lo studio dei fenomeni ereditari (o sistemi con memoria) nasce dall'osservazione che le deformazioni di un corpo elastico dipendono anche da quelle precedenti e si rivolge a quei corpi che conservano un ricordo della loro storia e il cui stato futuro dipenderà dunque da quello presente ma anche dai precedenti. Si ha di nuovo un'interessante convergenza tra fatti sperimentali e strumentazione matematica: le equazioni di campo non sono più equazioni differenziali ma integro-differenziali (che verranno in particolare applicate all’elettrostatica e all’elasticità ereditaria), dato che l'ereditarietà viene espressa da funzionali che sono integrali – rispetto al tempo – di combinazioni lineari delle componenti della deformazione.
4. L'Analisi
Parlando di Volterra, viene naturale passare agli studi di Analisi. La terza grande disciplina della Matematica ottocentesca si sviluppa in Italia soprattutto a Pisa. Il caposcuola, lo si è detto, è Ulisse Dini, laureatosi con Betti nel '64 con una tesi di Geometria differenziale. Il suo nome23 è universalmente noto – ai matematici e agli studenti di Matematica – vuoi per il teorema sulle funzioni implicite vuoi per la nozione di derivata di Dini, in cui l'usuale passaggio al limite è generalizzato attraverso le nozioni di limite superiore o inferiore. Ancora sono da ricordare i suoi studi sulle serie numeriche e trigonometriche, sulle funzioni di variabile complessa, sulle equazioni differenziali. Ma l'impatto maggiore che Dini ha sull'ambiente matematico italiano (e non solo quello) è legato alla pubblicazione della monografia Fondamenti per la teorica delle funzioni di variabili reali (1878) in cui sviluppa il suo programma rigorista: non si tratta di dimostrare nuovi risultati quanto, piuttosto, di porre quelli già noti su basi e fondamenta più solide, completandoli e precisando il loro dominio di validità.
Giuseppe Peano (1858-1932), torinese, è un altro dei protagonisti della svolta rigorista. Vi contribuisce con la presentazione degli assiomi dell'Aritmetica, con alcuni controesempi – spesso feroci nella loro semplicità – attraverso cui denuncia ipotesi sovrabbondanti, errori e inesattezze (presenti anche nei manuali più diffusi) e con una formulazione precisa e più generale di alcune nozioni fondamentali dell'Analisi (limiti, area di una superficie, formula di Taylor, derivate parziali, massimi e minimi per funzioni di più variabili reali, ecc.). Anche nel caso di Peano, siamo in presenza di un matematico universalmente noto24: il ruolo che occupa nella storia dell'assiomatizzazione delle teorie matematiche non è in discussione; la sua definizione, non ricorsiva, di derivata viene ancor oggi usata in talune ricerche di Analisi e di Ottimizzazione non-smooth; il suo contributo (della seconda metà degli anni ’80 dell'Ottocento) al teorema di esistenza per l'equazione differenziale y' = f(x,y), dimostrato con la sola condizione della continuità della funzione f, è specificamente menzionato in molti manuali; ugualmente riconosciuta è la sua priorità nell'individuazione di un sistema di assiomi per gli spazi vettoriali, in una monografia dedicata alla diffusione delle idee di H.G. Grassmann. La “curva di Peano” (1890) rimane, a distanza di più di 100 anni, una delle conclusioni più “sconvolgenti” e meno intuitive a cui il rigore deduttivo ha portato nella teoria degli insiemi e ha svolto un ruolo davvero significativo nella storia del concetto di dimensione: è possibile trovare una curva, espressa tramite due funzioni continue x = f(t) e y = g(t) che passa per tutti i punti del quadrato unitario, mentre t varia nell’intervallo [0,1], ovvero non è sempre possibile racchiudere un arco di curva continua in un'area arbitrariamente piccola.
Proprio sul tema del rigore, Peano ha una vivace polemica nel 1891 con Segre (e Veronese). A Segre che propende per una posizione meno rigida, e distingue il periodo della scoperta da quello di una successiva giustificazione rigorosa, replica seccamente che un teorema è scoperto solo quando è dimostrato e che, in mancanza dell'unico – assoluto – rigore che la Matematica conosce, si potrà fare della poesia (ma non della Matematica). Un'altra polemica, molto più aspra, Peano deve affrontarla con Volterra. Il contenuto matematico della disputa25 riguarda il moto di … un gatto, lasciato cadere nel vuoto con le zampe rivolte verso l'alto, e più in generale i moti interni di un corpo (e la possibilità di modificarne l'orientamento) che Volterra aveva analizzato con specifico riferimento al globo terrestre. Per ironia della sorte, qui è Peano ad essere messo sul banco degli accusati per il suo scarso rigore e la scarsa originalità delle conclusioni. La polemica acuisce il suo isolamento. Anche per gli esiti quasi naturali della sua battaglia rigorista, Peano abbandona progressivamente il campo della ricerca in Analisi e sviluppa l'ambizioso progetto di riconsiderare il complesso delle proposizioni della Matematica classica, per scomporle e analizzarle nei loro minimi elementi costitutivi ed essere così certi che in esse non compaia nulla di meno e nulla di più del necessario. Le stesse proposizioni verranno riscritte utilizzando combinazioni di segni algebrici e logici, che non lascino spazio ad alcun fraintendimento ma permettano una formulazione precisa e concisa.
Con Volterra possiamo tornare a Pisa, che abbiamo descritta come principale centro dell'Analisi italiana. L'influenza di Dini sul giovane Volterra è ravvisabile in un primo famoso contributo del 1881, all'età di soli 21 anni. All'interno del processo di completamento della teoria dell'integrazione secondo Riemann, uno dei principali motivi di interesse era costituito dai cosiddetti due teoremi fondamentali del Calcolo ovvero dallo studio dei rapporti tra le operazioni di derivazione e di integrazione. È in questo quadro che Volterra dà l'ormai classico esempio di funzione derivabile in un intervallo, con derivata limitata ma non integrabile. Poi gli orizzonti della ricerca si allargano, oltre le cornici di un programma rigorista. Volterra è attratto – anche per l'influenza di Betti e le sue sensibilità fisiche – dalla possibilità di applicare gli strumenti analitici, naturalmente in modo sofisticato e comunque adeguato alle esigenze del problema affrontato.
Sono queste le caratteristiche che ritroviamo nei suoi lavori di Analisi funzionale. Di questa disciplina e del suo sviluppo autonomo, Volterra può essere considerato a pieno titolo uno dei padri fondatori. Abbiamo già detto della sua impostazione “classica“, parlando della ricerca in Fisica-matematica. In Analisi funzionale, Volterra utilizza un linguaggio astratto e molto lontano dalla concretezza delle applicazioni ma sempre avendo davanti a sé, come punto di riferimento, problemi fisici o altre “applicazioni” matematiche. Sono questi che suggeriscono la particolare astrazione da seguire e costituiscono un momento di verifica della significatività della formalizzazione adottata. Le prime Note di Analisi funzionale sono della fine degli anni ‘80. Nel giro di pochi anni, Volterra introduce il concetto di funzionale con il relativo calcolo, fino allo sviluppo con un polinomio di Taylor. In realtà, non usa il termine di funzionale (che verrà suggerito successivamente da Hadamard) bensì quello di funzione di linea, per indicare un numero reale che dipende da tutti i valori assunti da una funzione y(x) definita su un certo intervallo ovvero dalla configurazione di una curva. Un funzionale è visto come caso limite, per n + +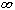 , di una funzione di n variabili. Si realizza così un primo progetto organico di studio degli spazi a infinite dimensioni e di trasferimento a determinati spazi funzionali dell’intero edificio dell'Analisi classica. La genesi di una simile generalizzazione, a partire dagli spazi n-dimensionali, viene enfatizzata e svolge un ruolo esplicativo e nello stesso tempo rassicurante. Siamo alla fine dell'Ottocento. Ancora pochi anni e arriverà la tesi di M. Fréchet, del 1906, che considera ancora specifici spazi funzionali ma già nella prospettiva di una teoria generale. , di una funzione di n variabili. Si realizza così un primo progetto organico di studio degli spazi a infinite dimensioni e di trasferimento a determinati spazi funzionali dell’intero edificio dell'Analisi classica. La genesi di una simile generalizzazione, a partire dagli spazi n-dimensionali, viene enfatizzata e svolge un ruolo esplicativo e nello stesso tempo rassicurante. Siamo alla fine dell'Ottocento. Ancora pochi anni e arriverà la tesi di M. Fréchet, del 1906, che considera ancora specifici spazi funzionali ma già nella prospettiva di una teoria generale.
L'altro ben noto contributo di Volterrra tra Ottocento e Novecento riguarda le equazioni integrali, per la prima volta inquadrate in quella teoria generale che verrà poi sviluppata da E. Fredholm, D. Hilbert e altri. Anche in questo caso – Volterra si occupa di equazioni integrali di prima e di seconda specie, con nucleo triangolare – il procedimento risolutivo è accompagnato dalla formulazione del principio del passaggio dal discreto al continuo, per il quale un'equazione integrale di prima specie è il caso limite (per n + +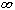 ) di un sistema di n equazioni algebriche in n incognite. ) di un sistema di n equazioni algebriche in n incognite.
Sempre a Pisa si laureano Giulio Ascoli26, Cesare Arzelà27 e Salvatore Pincherle che abbiamo già citato. I primi due nomi si trovano citati in ogni testo di Analisi funzionale. Pincherle, dopo la laurea, continua i suoi studi a Pavia (con Casorati) e soprattutto a Berlino, con K. Weierstrass28. Il soggiorno tedesco è essenziale per comprendere le linee di sviluppo della ricerca di quello che può essere considerato un altro dei pionieri dell'Analisi funzionale, attraverso il particolare riferimento fornito dalla teoria delle funzioni analitiche. La constatazione che ognuna di queste può essere individuata da un'infinità numerabile di parametri, interpretabili come sue coordinate, porta Pincherle alla considerazione di spazi funzionali di dimensione infinita e allo studio astratto dei funzionali lineari che agiscono su questi spazi, nel tentativo di costruire per questi funzionali un calcolo simile a quello ormai noto per le funzioni di una variabile complessa. Queste nozioni subiranno nel giro di pochi decenni sviluppi e approfondimenti impensabili, ancora all'inizio del secolo, anche lungo direzioni diverse. Quella percorsa da Pincherle non sarà forse la più affollata, come lui stesso avrà modo di riconoscere serenamente.
Dopo il breve soggiorno a Berlino, Pincherle si trasferisce definitivamente a Bologna (a parte la breve parentesi siciliana), che diventa con Pisa un nuovo centro significativo per le ricerche in Analisi. L'esponente più rappresentativo della scuola bolognese è Leonida Tonelli (1885-1946), uno dei massimi protagonisti della Matematica italiana nel periodo tra le due guerre mondiali29. Studia, con Arzelà e Pincherle, a Bologna dove si laurea nel 1907. La sua carriera accademica – come professore ordinario – per diversi motivi comincia però solo dopo la guerra (a Bologna e a Pisa). Ma già prima del 1915, Tonelli scrive lavori molto importanti – tra i più significativi della sua produzione – almeno nel campo dell'Analisi reale e del Calcolo delle variazioni. È del 1908 una Nota30 sulla lunghezza delle curve continue rettificabili, con particolare riferimento al caso in cui le funzioni che rappresentano la curva siano assolutamente continue. È del 1909 un’altra Nota31 che, per generalizzare la formula di integrazione per parti alle funzioni di due variabili, dimostra un criterio per l'integrabilità (secondo Lebesgue) di una funzione f(x,y) ³ 0 misurabile e dotata di una coppia di integrali successivi; l'articolo completa (teorema di Fubini-Tonelli) il noto risultato dimostrato da Fubini nel 1907, per cui l'integrale doppio (supposto esistente) di una f(x,y) può essere calcolato mediante due successivi integrali semplici, indipendentemente dall'ordine di integrazione.
Le sue Memorie fondamentali sul Calcolo delle variazioni sono del 1911, del 1914 e del 191532, ma sul Calcolo delle variazioni dei metodi diretti avremo modo di ritornare.
Giuseppe Vitali (1875-1932) è l'altro principale esponente della scuola bolognese, anche se si laurea a Pisa (dopo aver studiato a Bologna con Arzelà ed Enriques)33. È il 1905, in particolare, l'anno “magico” della sua produzione. Dopo aver provato la condizione necessaria e sufficiente per l'integrabilità secondo Riemann di una funzione limitata su un intervallo limitato (in dipendenza dalla misura dell'insieme dei suoi punti di discontinuità), Vitali pubblica in quell'anno una serie di Note in cui dimostra il cosiddetto teorema di Lusin sulla quasi-continuità delle funzioni misurabili, dà il famoso esempio di insieme non misurabile (secondo Lebesgue) e, ancora, caratterizza le funzioni integrali di funzioni non necessariamente limitate inaugurando il termine di funzione assolutamente continua (e studiando la classe di tali funzioni, in relazione a quelle a variazione limitata). Molti di questi risultati sono sostanzialmente contemporanei a quelli di H. Lebesgue, anche se ottenuti in modo del tutto indipendente. Bisogna a questo proposito ricordare che Vitali, dopo la laurea, non riesce a trovare una sistemazione universitaria ed è costretto per molti anni all'insegnamento medio, in sedi periferiche, al di fuori di qualsiasi canale di comunicazione scientifica. D'altra parte, anche Lebesgue si lamenta che a Poitiers – dove insegna dal 1906 al 1910 – non gli è possibile consultare alcuna rivista italiana. Questo spiega la parziale sovrapposizione dei risultati di Vitali con quelli del matematico francese, ma non toglie originalità e valore alla sua ricerca e, in particolare, a quella sulle funzioni assolutamente continue; qui la sua priorità è chiara, non tanto per l’introduzione del termine e neanche per la generalizzazione alle funzioni di due variabili, quanto proprio per la centralità assegnata a tale nozione nella teoria dell'integrazione.
La primavera della Matematica italiana all'inizio del Novecento non si limita alla Geometria, alla Fisica matematica e all’Analisi ma coinvolge anche le “nuove” discipline. Abbiamo già detto come Peano sia condotto agli studi di Logica dalla sua battaglia rigorista e dalla ricerca della massima precisione nelle definizioni e nelle dimostrazioni, anche in funzione didattica. Attorno a lui – ai suoi progetti editoriali e alla Rivista di Matematica (fondata nel 1891) – si coagula rapidamente una scuola di giovani e battaglieri studiosi. La loro presenza anima molti di quei Convegni che caratterizzano, innovativamente, l'inizio del secolo. L'incontro con Peano, al Congresso Internazionale di Filosofia, a Parigi, nel 1900, verrà ricordato da Bertrand Russell come particolarmente significativo per la formulazione del suo programma. In parziale contro-tendenza con quanto si stava affermando, la Logica matematica non è per Peano applicazione di tecniche algebriche alla Logica tradizionale (e non è quindi – neppure in prospettiva – disciplina matematica autonoma) ma strumento e linguaggio funzionali all'attività matematica, per esprimere con la massima chiarezza concetti e dimostrazioni.
Con ancora minori tradizioni, si forma anche un gruppo di giovani economisti matematici. La “lezione” di Walras è fatta propria da Vilfredo Pareto (1848-1923) che, sia pure dalla cattedra di Losanna, è il fondatore della scuola italiana di Economia matematica e il vero divulgatore della teoria dell'equilibrio economico generale. L'Economia matematica tende a diventare una disciplina autonoma. Vive però ancora in stretto dialogo con gli altri ambiti di ricerca matematica e con quei settori della cultura e della società italiana interessati al tentativo di matematizzare una scienza tradizionalmente considerata nel campo di quelle morali, dandole fondamenti quantitativi e “oggettivi”34. La stagione più viva dell'Economia matematica italiana è breve, molto legata alla parabola di Pareto che nel 1909, con la pubblicazione dell'edizione francese del Manuale di Economia politica, cesserà di fatto le sue ricerche in ambito economico. Ciò non impedirà ad un economista e ad uno storico dell'Economia, quale Joseph Schumpeter, di valutare che la ricerca economica italiana (proprio grazie agli economisti matematici) non era nel 1915 seconda ad alcuna.
5. Proiezioni esterne
Per la generazione risorgimentale abbiamo parlato di un piccolo gruppo di matematici di valore, temprati e selezionati dalle vicende militari e politiche, che prolungano nella ricerca il loro impegno civile prendendo a modello le realtà europee più avanzate. Adesso, il piccolo gruppo è cresciuto. Abbiamo presentato i ricercatori più affermati, incontrando di fatto (quasi) tutti quelli che saranno protagonisti della nostra storia: Enriques e Severi; Levi-Civita e Volterra; Tonelli. Sono aumentate le cattedre di Matematica; è aumentato il numero di giovani, che aspira ad una carriera universitaria. In attesa di una Società nazionale di matematici, si sviluppano accademie e associazioni scientifiche (spesso accompagnate dalla pubblicazione di riviste e “bollettini”). Nel 1870, con la presa di Roma, si avvia la ristrutturazione della storica Accademia dei Lincei. Nel 1884 viene costituito il Circolo Matematico di Palermo, che presto si imporrà all'attenzione del mondo matematico come è la più importante organizzazione matematica mondiale!
Anche se l'aumentata consistenza della comunità scientifica rende improponibile il modello di una mente collettiva che elabori e attui un unico piano, ugualmente, il quadro più articolato che abbiamo davanti, all'inizio del nuovo secolo, si presta ad una lettura sufficientemente omogenea. Gli sforzi per un sempre più marcato inserimento nel contesto internazionale rimangono costanti (come prova anche la storia esemplare del Circolo matematico di Palermo), così come permane un forte impegno civile. La sempre maggiore complessità sociale non permette però che esso si esprima solo attraverso la presenza nel governo e nelle assemblee parlamentari. Occorre un maggior numero di passaggi. Si deve mettere in conto una lunga marcia all'interno della società.
Un simile viaggio, per la Matematica, non può che cominciare dal mondo della scuola. I gravi problemi dell’istruzione, segnalati all'indomani dell'Unità, non trovano in generale soluzione. Il processo di omogeneizzazione delle diverse realtà regionali è lento; quello di modernizzazione del Paese appesantisce il mondo della formazione di ulteriori compiti e obiettivi. Nelle scuole secondarie, l'esigenza di aumentare i tassi di scolarizzazione scatena diverse pressioni (anche e soprattutto nei confronti della Matematica) volte a ridurre e semplificare i programmi. A livello universitario, la presenza di troppe sedi – ereditata dagli stati pre-unitari – pone il problema della qualità dell'insegnamento.
A questo stato di cose e a queste innegabili difficoltà, gli insegnanti di Matematica rispondono positivamente, con un forte impegno individuale e la creazione (nel 1895) di una società – la Mathesis, che cura la pubblicazione del Periodico di Matematiche – cui collaborano anche diversi docenti universitari. I risultati non saranno sempre in linea con gli sforzi profusi, come testimoniano anche le varie crisi che l'associazione si troverà successivamente a gestire. Colpisce comunque della Mathesis, in questi anni, la grande fiducia nella possibilità di un coinvolgimento attivo e diretto dagli iscritti e nella riuscita di un movimento di riforma dal basso. Tutte le principali questioni didattiche vengono – con piglio positivo – enunciate, numerate e sottoposte alla consultazione tra gli insegnanti. La forza della rappresentatività e della ragione dovrebbe poi quasi inevitabilmente, negli auspici della Mathesis, trasformare le soluzioni trovate in un progetto di riforma.
Il viaggio della Matematica italiana verso il suo esterno non si limita a radicare e diffondere la propria cultura nelle giovani generazioni, ma tende ad “esportare” il linguaggio e la razionalità che ritiene caratteristici del proprio mondo, toccando anzitutto le discipline scientifiche tradizionalmente più vicine. Dal 1895 Il nuovo cimento diventa l’organo della Fisica italiana e Volterra fa parte del ristretto Comitato scientifico della rivista. Due anni dopo, viene costituita la Società italiana di Fisica e ancora Volterra – come abbiamo avuto modo di ricordare – ne è presidente.
Ancora più sorprendenti sono le “incursioni” nei terreni presidiati dall'“altra” cultura. Il fatto che i matematici sviluppino una discreta sensibilità storica ed esprimano la loro opinione anche su questioni di natura filosofica non può passare sotto silenzio, pur in presenza di una cultura ancora fortemente unitaria, nella quale non si sono ancora scavati in profondità quei solchi che caratterizzeranno il pensiero del Novecento.
Il personaggio più esposto è qui Enriques. Le prime testimonianze dei suoi interessi filosofici – o della ripresa di quelli già intravisti, da studente liceale – risalgono a metà degli anni ’90, ma è nel nuovo secolo che la presenza di “Enriques filosofo” diventa pubblica e significativa. Nel 1906, viene dato alle stampe il volume I problemi della scienza. Enriques affronta tutta una serie di questioni, attentamente studiate da matematici quali F. Klein e H. Poincaré, traendo spunto dall'analisi della costruzione dei sistemi geometrici e del problema dello spazio: qual è la natura dei postulati geometrici? come spiegare, da questo punto di vista, le diverse Geometrie? Nella sottolineatura del ruolo dell'intuizione e delle interazioni sussistenti tra spazio reale, intuizione spaziale e postulati della Geometria, c'è il rifiuto di Enriques a considerare quest'ultima come un sistema puramente formale. I postulati della Geometria sono astrazioni concettuali, elaborate però in funzione delle diverse modalità della nostra intuizione spaziale. Sempre nel 1906, Enriques fonda la Società filosofica italiana (SFI) di cui è primo presidente; l'anno successivo fonda la Rivista di Scienza, che dal 1911 assumerà il nome di Scientia e si propone come periodico internazionale di sintesi scientifica, per ovviare ai pericoli derivanti dall’eccesso di specializzazione. Sempre nel 1907 interviene al secondo Congresso della SFI con una relazione intitolata Il rinascimento filosofico nella scienza contemporanea, mentre in quello successivo fa addirittura i conti con Hegel con la relazione La metafisica di Hegel considerata da un punto di vista scientifico. È chiaro che a questo punto la sua presenza non può essere più ignorata dai filosofi “professionisti” e, in particolare, da Benedetto Croce (1866-1952) e da Giovanni Gentile (1875-1944), esponenti di punta dell'idealismo italiano e già all'inizio del secolo portatori di un progetto di egemonia sulla cultura del Paese. L'occasione del redde rationem è rappresentata dal IV Congresso Internazionale di Filosofia (1911), assegnato all'Italia e quindi organizzato e presieduto da Enriques (come presidente della SFI). I dissensi con Croce e Gentile cominciano presto, già durante la preparazione dei lavori. Poi questi si svolgono regolarmente. È alla loro chiusura, in un'intervista rilasciata a un quotidiano, che Croce si scaglia pubblicamente contro Enriques, accusandolo senza mezzi termini – con frasi ironiche e giudizi pesanti – di dilettantismo e di invasione di un campo che non conosce assolutamente. La stroncatura di Croce è emblematica: con una dichiarazione di incomunicabilità e di ostilità, la cultura ufficiale – o comunque quella più radicata nelle tradizioni del Paese – emette un giudizio negativo (destinato a “contare” per molti decenni) sul generoso tentativo dei matematici di coniugare la loro alta professionalità con una cosciente partecipazione alla vita culturale e sociale del Paese.
Se la polemica Croce–Enriques rimane forse l'episodio più noto di questa stagione, quello più “politico” vede protagonista ancora Volterra, con la fondazione (già citata) della SIPS. La società nasce con quel duplice obiettivo, già visto a proposito della Mathesis. Quello interno riguarda la comunità scientifica e la presa di coscienza del proprio ruolo intellettuale. La specializzazione degli studi è una necessità che non deve comportare fratture totali e l'isolamento in mondi angusti, animati solo da una dimensione tecnica. La coscienza di una missione più ampia e un'immagine più accattivante (da raggiugersi attraverso la divulgazione delle personalità degli scienziati e delle modalità del loro lavoro) sono la necessaria premessa per una forte pressione sui poteri politici contro il loro immobilismo, perché riconoscano l’utilità sociale della scienza e sappiano trovare una giusta collocazione al mondo scientifico. Questo è il secondo obiettivo della SIPS: concorrere allo sviluppo di un Paese moderno, che riconosca la funzione sociale della scienza, nella direzione già assunta dalle nazioni europee più evolute. Il messaggio è lucido e forte. Volterra propone se stesso e la comunità scientifica per un ruolo dirigente nello sviluppo del Paese, espressione di un modello di razionalità e di un’organizzazione sufficientemente forti da poter controllare e risolvere le contraddizioni della propria crescita. Anche di questa rivendicazione si deve tener conto nel descrivere la Matematica italiana negli anni tra le due guerre mondiali.
Conclusione
Sembra opportuno chiudere questa prima sezione con l'accennare ad alcune implicazioni storiografiche della “esplosione matematica” prima sommariamente descritta, non dissimile da quella che avviene in Polonia all'indomani della grande guerra e sul cui sfondo proietteremo poi il tendenziale declino della Matematica italiana nel periodo tra le due guerre.
Come è stato possibile, a partire da una situazione pre-risorgimentale fortemente disomogenea e certamente di basso profilo su scala internazionale, ottenere simili risultati?
Una tradizione storiografica consolidata, inaugurata da Vito Volterra (1860-1940) nella seduta plenaria di apertura del già citato IV Congresso internazionale dei Matematici, ha sostanzialmente convalidato la tesi che al Risorgimento politico del paese si era accompagnato un vero e proprio Risorgimento scientifico (in particolare, matematico). Non che si negasse una presenza matematica negli anni pre-unitari e, almeno in qualche sede – Pavia e Pisa soprattutto, ma per certi versi anche Torino, Roma e Napoli – ad un livello tutt'altro che spregevole, ma porre l'accento sulla “rottura” operata dal processo unitario piuttosto che sulla “continuità” con la tradizione precedente, aveva il significato di sottolineare maggiormente gli aspetti “esterni” alla disciplina rispetto a quelli ad essa “interni”.
Il consenso su questa tesi storiografica è, ripeto, unanime. Essa, nell'arco di tempo che va dal citato discorso di Volterra all'Abregé di (Dieudonné, 1978), piuttosto che mutare si è via via precisata, sempre però sottolineando che il dato più significativo, e anche più problematico, è il processo con cui avvenne il rilancio della matematica italiana, che potè godere di un clima generale favorevole alla partecipazione degli scienziati, e dei matematici in particolare, alla guida politica del paese. Quasi non ci fu soluzione di continuità tra i “bisogni” legati ad una moderna organizzazione scientifica – l'istituzione di nuove cattedre di matematiche superiori, una radicale riforma dell'insegnamento medio e superiore o l'istituzione di nuovi centri d'istruzione superiore come il Politecnico di Milano, voluto e diretto da Francesco Brioschi dal 1863 fino alla morte – e il momento della decisione politica.
A quanto già detto vanno almeno aggiunti due altri elementi, entrambi presenti nella già citata analisi di Volterra: da un lato, il collegamento internazionale dei matematici italiani della seconda generazione, che seppero cogliere nella letteratura dell'epoca i problemi più nuovi e più fecondi, e, dall'altro, un vivace e talvolta aspro dibattito sul modo di concepire la Matematica.
Molteplicità d'indirizzi e/o di linguaggi, attenzione a tutto ciò che di nuovo avveniva all'estero, presenza di un clima generale di rinnovamento che alle scelte tecnologiche e scientifiche legava buona parte degli esiti “risorgimentali”, assenza infine di tradizioni di ricerca “forti” o di “egemonie” capaci di ostacolare, come invece avverrà nel periodo tra le due guerre, lo svilupparsi di nuove tendenze, sono questi gli elementi che favorirono l'“esplosione” della matematica italiana. Non in altri termini si esprimeva Enrico Bompiani nella sua ricostruzione (manoscritta) del primo mezzo secolo di vita matematica unitaria fatta in previsione della progettata “Esposizione universale di Roma” del 1942 (Israel, Nastasi, 1998).
Resta ovviamente la difficoltà epistemologica di conciliare l'attività matematica, di natura prettamente individuale, con i condizionamenti provenienti dalla sfera sociale, tema su cui il dibattito è del tutto aperto non apparendo fondanti le considerazioni di (Dieudonné, 1978, p. 9) o quelle di chi si è posto il problema di descrivere una “esplosione” non dissimile da quella italiana, l'emergere cioè ed il formarsi, nel periodo tra le due guerre, della vivace scuola matematica polacca cui si deve, fra l'altro, lo sviluppo di non pochi rami della Topologia e dell'Analisi funzionale.
Ma è preferibile ormai soffermarsi su quest’ultimo aspetto – legato al fenomeno, gia sollevato da Volterra, dell'alternarsi di centri matematici di forte attività – che si può considerare come l'anello di congiunzione tra il primo e il secondo periodo e che introdurrà gli elementi di analisi utili per giustificare la seconda delle affermazioni iniziali, quella cioè relativa al tendenziale declino della Matematica italiana nel “ventennio” intercorso tra le due guerre.
|

